ازاي تحسب الانحراف المعياري في اكسل؟
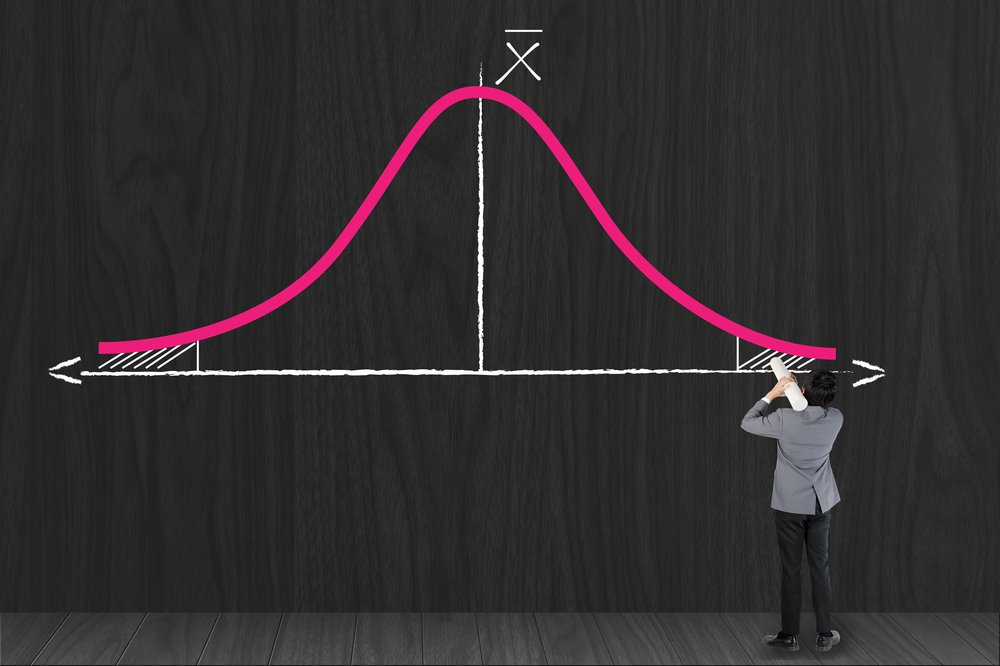
الانحراف المعياري هو مصطلح في الإحصاء بيوضح الفرق بين المتوسط والبيانات الفعلية، وبيساعدنا نفهم إذا كانت البيانات ثابتة ولا متشتتة، الانحراف المعياري بيكون عالي لما البيانات تكون متشتتة، وبيكون منخفض لما البيانات تكون متساوية.
لما تشتغل على مجموعة بيانات رقمية، بتحب تعرف العنصر القياسي بتاعها، تقدر تجرب تحسب المتوسط بتاعها أو تحسب الوسيط، بس المركزية مش بتدينا معلومات موثوقة عن البيانات.
إقرأ المزيد: 20 سؤال في Excel للمحللين الماليين لأي انترفيو
المتوسط هو مجموع كل الأرقام اللي في المجموعة مقسومة على عددهم.
الوسيط هو الرقم اللي في النص لما ترتب المجموعة من الأقل للأعلى.
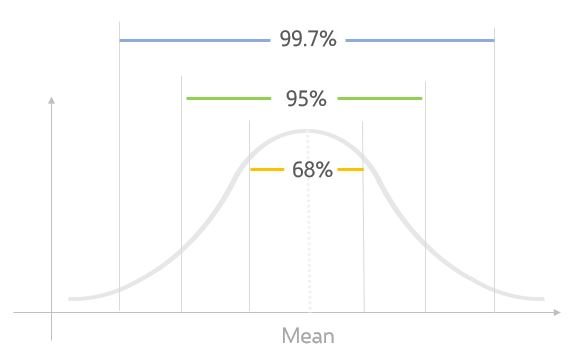
الانحراف المعياري بيبين إذا كانت الأفراد في مجموعة البيانات دي متساوية ولا لأ، فبيكون استخدامه شائع ومهم جدًا.
إزاي تحسب الانحراف المعياري رياضياً؟
دلوقتي هوضحلك ازاي تحسب الانحراف المعياري بمثال بسيط جداً، لو عندك مجموعة من البيانات الرقمية: 4، 6، 8، 12، 15.
أول حاجة لازم تحسب المتوسط من خلال جمع كل الأرقام وتقسيمهم على عدد الأفراد في المجموعة، في حالتنا دي، المتوسط هو 45/5، يعني 9.
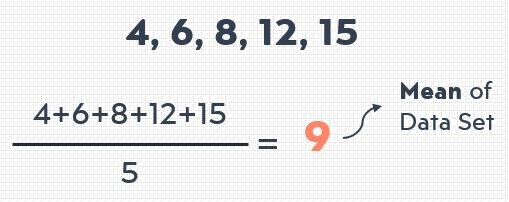
بعدين، هتطرح كل الأرقام من المتوسط وتربع الفرق بالعدد نفسه عشان تبقي كل النتايج موجبة بدل من سالبة، بعدين بتجمع كل الأرقام اللي اترفعت للمربع مع بعض وتقسمها على واحد أقل من عدد الأفراد في مجموعة البيانات (واللي هو 4 في المثال ده).
بعدين تأخذ الجذر التربيعي للمعادلة، وخلاص! حسبت الانحراف المعياري، النتيجة هي 4.

ليه الانحراف المعياري مهم؟
الانحراف المعياري مهم جدا في حاجات زي المسائل المالية، مش هتقدر تحسب المخاطر بس بمجرد انك تشوف المتوسط، ده ممكن يديك رأي سطحي عن البيانات بس مش كفاية ولا المعلومات كمان بشكل كافي.
لو افترضنا إنك عايز تستثمر فلوس في شركة وهما بيقولولك إن المستثمرين جابوا ٣٠٪ ربح في نهاية السنة، البيانات دي هتقولك إن الربح ممكن يكون بين -٢٠٪ و ٨٠٪.

لو قدمت على شغل وقالولك إن متوسط راتب الموظفين في الشركة ٢٠٠٠٠ دولار، ده ممكن يبان حاجة كويسة، بس ايه اللي هيحصل لو كانت الرواتب متفاوتة من ١٠٠٠ دولار لـ ١٩٠٠٠ دولار؟
كمان مستحيل تقارن بين مجموعات بيانات بدقة من غير ما تستخدم الانحراف المعياري، فلو افترضنا إن عندك مجموعتين من البيانات ليهم نفس المتوسط. الأولى فيها الأرقام 600، 30، 0 والتانية فيها الأرقام 299، 210، 2100، لما تشوف المتوسط هتلاقيهم نفس الحاجة، بس الانحراف المعياري بينهم كبير جدًا. المجموعة الأولى غير موثوقة والتانية متسقة.

باختصار، الانحراف المعياري مهم لأنه:
- عنصر أساسي لحساب حدود الخطأ.
- بيسمحلنا نقارن مجموعتين مختلفتين من البيانات بفعالية.
- بيظهر لينا المخاطر من خلال عرض نطاق البيانات.
استخدام الانحراف المعياري في الحياة الواقعية:
ناس كتير بيستخدموا الـ standard deviation ده كل يوم في حياتهم فعلًا. الإحصاء ده بيديك رأي واضح عن الفروق اللي في بياناتك، فبيبقى مفيد جدًا، والحقيقة في أمثلة كتير من حياتنا اليومية بيستخدموا الانحراف المعياري ده، وده هيساعدك تفهم أهميته، زي:
1- لما بتحسب المدى للمتوسط الحسابي في مجموعة بيانات:
مثال: عندك فصل من طلاب مدرسة اخدوا امتحان فيزياء، وبعد ما الأستاذ حسب المتوسط الحسابي للدرجات، لقى إنه 75%، بعد كدة الأستاذ قرر يحسب الانحراف المعياري عشان يعرف اذا كانت الدرجات متقاربة من الـ 75% ولا لأ.
وطلع إن الانحراف المعياري كان صغيرة جدًا، يمعني إن درجات الطلاب كانت قريبة جدًا من الـ 75%.

مثال تاني: فصل من طلاب المدرسة اخدوا امتحان في اللغة الإنجليزية. بعد الامتحان، قررت المدرسة إن متوسط الدرجات كان 55%، ولما شافت إن النتيجة كانت منخفضة جدًا، قررت إنها تحسب الـ standard deviation عشان تعرف عدد الطلاب اللي درجاتهم كانت قريبة للمتوسط.
طلع إن الـ standard deviation كان كبير، بعد ما فحصت كل الاختبارات كويس، لقت إن في طلاب كتير بدرجات منخفضة جدًا كانوا السبب في إن المتوسط الحسابي لدرجات الفصل كان منخفض جدًا.
2- عشان تلاقي القيم الطردية في مجموعة بيانات:
دكتور بيطري عايز يتأكد اذا كان وزن القطط اللي تحت رعايته قريب من بعضها ولا مش قريب، فقام حسب متوسط أوزان العشرة قطط (المتوسط الحسابي).

بعد ما خلص حساب الوزن المتوسط للقطط العشرة، حسب التقريب، جاب العدد اللي يقوله مدي اختلاف أوزان القطط عند بعضها، ولما حسب الانحراف المعياري، لقاه عالي جدًا، وده معناه إن القطط بتاعته مش بتوزن نفس الوزن، ممكن في بعضهم وزنهم أكبر من اللزوم، يعني في قيم طردية بتعمل فوضى في الداتا.
3- في حالة تحديد مدى موثوقية البيانات:
باحث متخصص في المتاجر بيدرس نتايج استطلاع رأي عملاء اتعمل مؤخرًا، وعايز يحدد مقدار موثوقية الإجابات اللي تم جمعها في الاستبيان عشان يتنبأ بكيفية إجابة عينة أكبر من الناس على نفس الأسئلة، هنا انخفاض الانحراف المعياري بيوضح ان الإجابات مناسبة جدًا للعينة الكبيرة.
مثال تاني هو لما يحلل مذيع الأحوال الجوية درجات الحرارة العالية المحسوبة لسلسلة من التواريخ مقابل درجة الحرارة العالية الفعلية المسجلة في كل يوم، هنا الانحراف المعياري المنخفض بيشير لتوقعات طقس موثوقة.
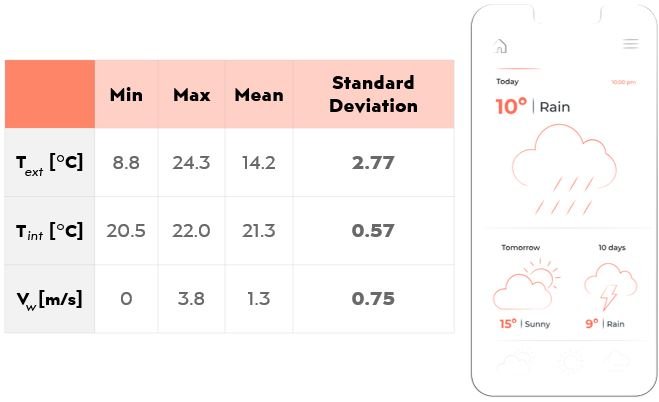
صاحب العمل عايز يعرف إذا كانت الرواتب في الإدارات بتاعته عادلة لكل الموظفين، ولا فيه فرق كبير، هو بيحسب متوسط الرواتب في الإدارة دي وبعدين يحسب التنوع، وبعدين الانحراف المعياري.
صاحب العمل لقي إن الانحراف المعياري أعلى من المتوقع، ففحص البيانات بتفصيل واكتشف إن في 3 موظفين كبار في السن، اشتغلوا في الإدارة لمدة 15 سنة أو أكتر، بيأخدوا رواتب أعلى بكتير من باقي الموظفين بسبب استمراريتهم مع الشركة.
عملية التحليل هنا ساعدت صاحب العمل على فهم مدى تباين الرواتب في الإدارة.
4- لما بيحددوا مقاس قياسي:
لما بيحددوا المقاييس القياسية في تصميم الإنتاج، بيحاولوا المصممين يطوروا نظام عام للأحجام عشان يحددوا الاختلافات اللي لازم تكون في حجم المنتج عشان يناسب كل الناس، زي القمصان مثلاً، أو كراسي الأطفال في السيارات. وعشان يعملوا كدا، المصممين بيستخدموا الانحراف المعياري عشان يحسبوا كام التفاوت اللي لازم يكون موجود في خط إنتاج المنتج.
الانحراف المعياري في الرياضة
ليه محتاجين نستخدم الإحصاءات في الرياضة؟ فكر فيها زي لو إنت مدير فريق:
- تقدر تشوف متوسط فريقك في بعض المؤشرات عن طريق الرسوم البيانية وتقارنه بالفرق التانية في الدوري.
- هتحدد الاتجاهات الصاعدة أو الهابطة بمقارنة بيانات فريقك مع بيانات مباريات الفرق التانية.
- هتقارن بيانات مباريات فريقك مع فرق تانية عشان تكتشف التغييرات التكتيكية.
- تقدر تشوف معدلات النجاح والفشل في مؤشرات الهجوم والدفاع والتمرير والمواجهات الفردية لفريقك بسرعة وتقارنها مع بيانات فرق تانية.
بتستخدم الأندية الرياضية الانحراف المعياري، مثلًا، فريق يكون دايمًا ناجح هتلاقي فيه انحراف معياري قليل، وفريق تاني بيسجل نتايج متفاوتة بيكون فيه انحراف معياري عالي.

في السنوات الأخيرة، ازداد استخدام الإحصاءات التحليلية في الرياضة، حتى ان شركة ESPN (منصة بث الرياضة المعروفة) أطلقت قسم جديد على موقعها الإلكتروني مُخصص للتحليل الرياضي، باين كده انه أصبح فيه اهتمام بتطوير مقاييس جديدة لقياس أداء الرياضيين بشكل يومي.
نظرية Moneyball
شفت فيلم Moneyball الأمريكي قبل كده؟ الفيلم عن فريق بيسبول (أوكلاند A’s)، اللي بدأوا يستخدموا البيانات الإحصائية عشان يطوروا أدائهم في المباريات، في الأساس ده بداية العالم الرياضي اللي بنعرفه النهارده، النهاردة جذب اللاعبين الممتازين للفرق أقل أهمية من جمع ومعالجة البيانات، لأن البيانات بتظهر للمدربين فين يقدروا يطوروا الفريق ويزودوا فرصتهم في الفوز بالبطولة (واللي بيتمناه كل مدرب).

الموضوع ده خلق نظرية اسمها نظرية الموني بول، النظرية بتجاوب سؤالين سهلين: هل اللاعب بيعرف يضرب الكورة؟ وهل اللاعب بيقدر يخلق نقط؟ لو الإجابة بأه، يبقى فريقك في أمان، وده اللي استخدمه مدير عام فريق أوكلاند A’s بيلي بين في سنة 2002. استخدم نظرية الموني بول عشان يختار فريق من اللاعبين المستهان بيهم.

هو وفريقه فازوا في ٢٠ ماتش على التوالي في الفترة من ٢٠٠٠ لغاية ٢٠٠٦، فريق أوكلاند إيهز فاز بمتوسط ٩٥ ماتش، وفاز بأربع ميداليات في الدوري الأمريكي الغربي، وظهر في خمس مباريات بلاي أوف.
مجرد افتراض من واحد حسب الانحراف المعياري وعالجه بشكلٍ مختلف بدل ما يكتفي بالمتوسط أو الملاحظة بالعين المجردة، غيّر بشكل كلي من عالم الرياضة الحالي.
إزاي تحسب الانحراف المعياري في برنامج إكسل:
دلوقتي، بما ان عندك معلومات عن الانحراف المعياري وطريقة استخدامه، ممكن تبدأ تتعلم طريقة حسابه في برنامج إكسل.

إكسل ده برنامج مكتبي بيساعدنا نحسب الداتا اللي احنا جمعناها، وموجود فيه أدوات للحسابات والرسم البياني وجداول البيانات المحورية، ولغة برمجة اسمها فيجوال بيسك للتطبيقات.، بس بتقدر تحسب الانحراف المعياري بسهولة باستخدام صيغ بسيطة.
خلينا نبدأ!
في إكسل موجود 8 صيغ عشان تحسب الانحراف المعياري، وبتقدر تحسب الانحراف المعياري لعينة أو لكل الداتا اللي عندك.
لو عايز تحسب الانحراف المعياري لعينة، استخدم: STDEV.S، STDEVA و STDEV.
أما لو عايز تحسب الانحراف المعياري لكل الداتا (المجتمع الكلي)، استخدم: STDEV.P، STDEVPA و STDEVP.
الحسابات بالعينات شايفينها كتير لأنه في بعض الأحيان مش ممكن نحسب كل البيانات، وعشان كده هنبتدي بصيغ حساب العينات.
STDEV.S – دي الصيغة اللي بنستخدمها لما تكون كل البيانات اللي عندنا بالأرقام وبتتجاهل النصوص والقيم المنطقية وقت الحساب
الصيغة دي متاحة في النسخ بعد 2007، ولو عندك نسخة قديمة بتقدر تستخدم STDEV بدالها.
STDEVA – ده لما تكون عايز تحسب النصوص والقيم المنطقية مع البيانات الرقمية. (في القيم المنطقية، الصفر معناه كاذب والواحد معناه صحيح.)
ازاي استخدم STDEV.S أو STDEV؟
عشان تستخدم STDEV.S، تدخل صيغة بسيطة جدًا:
…,TDEV.S(number1, number2, number3…) or STDEV.S([number1], [number2], [number3]
- رقم 1: دي الحجة المطلوبة في الصيغة. وهي أول عنصر في العينة. تقدر تستخدم مصفوفة واحدة، أو مجموعة باسم، أو مرجع لمصفوفة بدل ما تستخدم الفواصل.
- رقم 2 ورقم 3: دي خيارية، تقدر تزود الصيغة بأرقام تانية معاك لغاية 254 رقم في إكسل.
فلو عندك مجموعة بيانات درجات الامتحانات من A2 لـ A11، هتستخدم الصيغة دي ببساطة:
=STDEV.S(A1:A11)
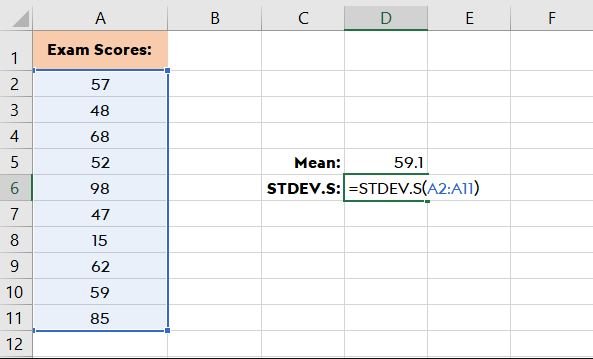
ولو عندك إصدار أقدم من إكسل، ممكن تستخدم STDEV بدل من STDEV.S، في نفس سيناريو STDEV.S، هتستخدم الصيغة:
=STDEV(A2:A11)
مهم: إزاي نحسب الـ Z Score في برنامج الاكسل؟
ازاي تحسب الانحراف المعياري يدوي؟
لو مش عارف تستخدم صيغ إكسل، ممكن تحسب الانحراف المعياري يدوي. هعرفك ازاي بالخطوات خطوة بخطوة.
فرضًا إنك دخلت البيانات من A2 لـ A11، بعد ما تدخل البيانات على برنامج إكسل، لازم تحدد الانحراف، بمعني إنك تحسب الفرق بين قيمة العنصر والمتوسط. والصيغة هي:
=A2 -AVERAGE($A$2:$A$11)
،قيم الانحرافات هتتحط في العمود B، وتبدأ من B

بعد ما تحسب الانحراف، هتحتاج تحسب قيمة الانحراف المربع، لو كان في قيم سالبة في الحسابات الأولى، القيم هتبقى كلها بالموجب. وعشان تحسب القيم المربعة للانحراف، هتستخدم الصيغة دي: =(B2)^2
،قيم الانحرافات المربعة هتتحط في العمود C، وتبدأ من C2.
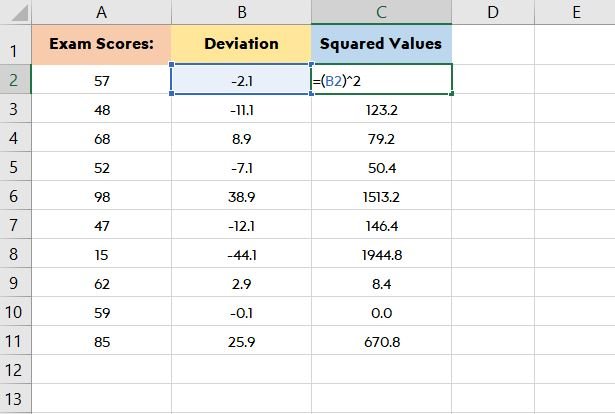
في الخلية E3 هتحسب الانحراف المعياري للمجموعة كلها باستخدام الصيغة دي:
=SQRT(SUM(C2:C11)/COUNT(C2:C11))
وفي الخلية E4 هتحسب الانحراف المعياري للعينة باستخدام الصيغة دي:
=SQRT(SUM(C2:C11)/(COUNT(C2 :C11)-1))

ودي كانت كل حكاية الـ Standard Deviation الانحراف المعياري، وطريقة حسابه في برنامج إكسل بطريقة سهلة وبسيطة.
متنساش تتواصل معانا في حال كنت عايز تسأل أو تستفسر عن أي حاجة بخصوص الانحراف المعياري وطريقة حسابه في الاكسل.